Skip to content

AB Testing Framework With Regression

category_specifier : "Causal Inference"

Reference Docs:Linear regression coefficient | Using Control Variables | Omitted Variable Bias | Instrument Variables | Diff-in-diff

Overview

💡How do we measure pure effect of treatment?

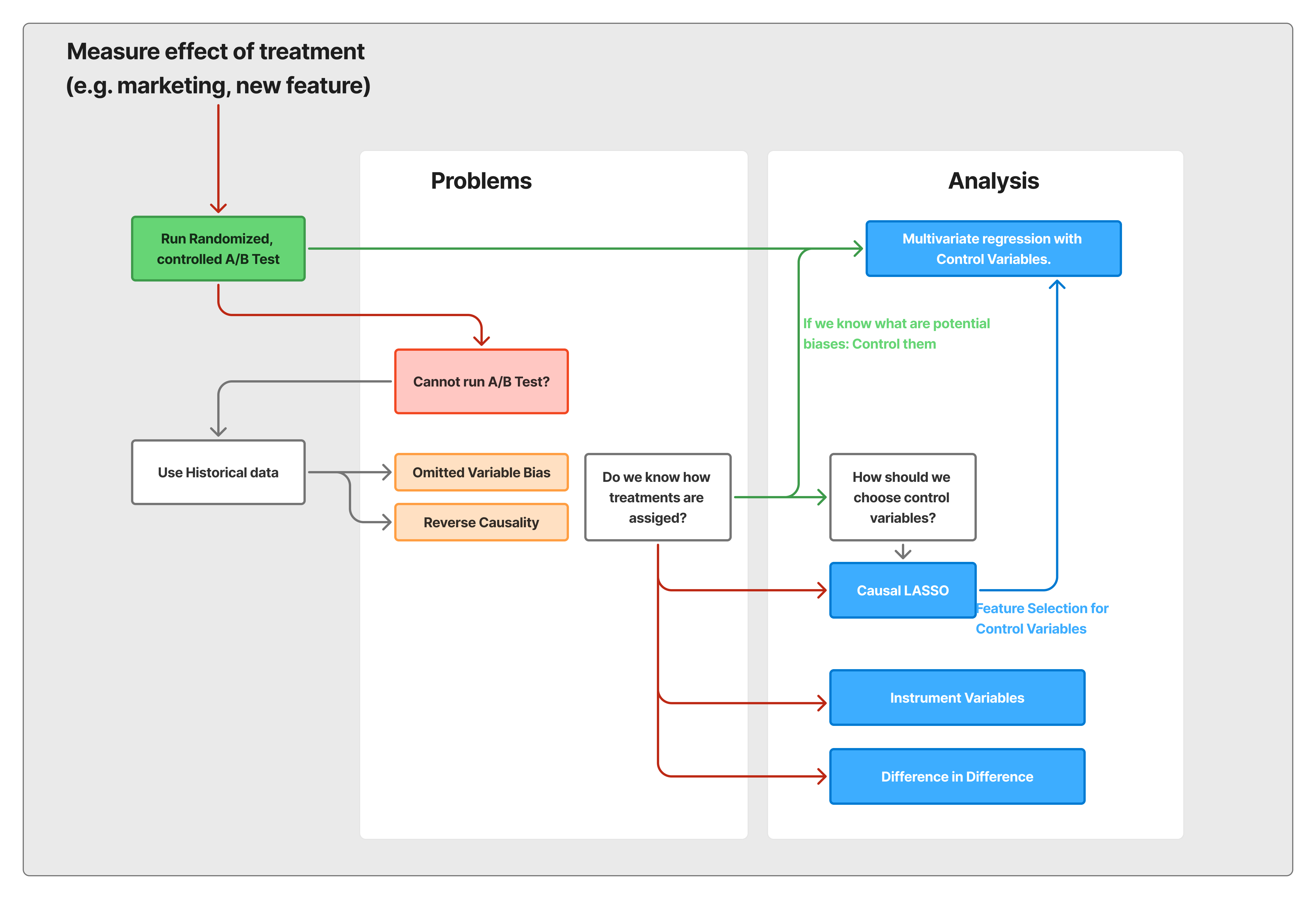
ab_regression_summary

  • Best way to measure effect of treatment (marketing event, new feature etc) is running randomized A/B Test
  • This is because, if assignment of treatment is not randomized, difference in result could be effected by other variables (bias) other than the treatment.
  • Linear regression coefficient is used to measure pure effect of treatments.
  • Why?: Coefficient of treatment vaiable implies the effect of treatment on dependent variable (y), fixing all the other variables constant.

Basic Framework Structure

regression_summary

  • Methodology: Run regression on variable of interest (\(y\)) over treatment dummy variable \(X_1\): $$ Sales = y = \beta_0 + \beta_1*\text{(Ad exposure dummy)}+ e $$

  • In the example above, \(X_1\) = 1 if the user is exposed to the ad, 0 if they are not exposed to the ad.

  • Interpretation of \(\beta_1\): Effect of 'Ad exposure' on increasing value of the sales. (How likely the sales will increase, when user is exposed to the ad?)
  • Interpretation of \(\beta_0\): Baseline expected sales, when user is not exposed to the ad. (When Ad exposure dummy = 0)

Problem of using single variate regression, and further bias control techniques.

  • Only relying on single variate regression, only using treatment dummy is both risky for using data from A/B test, and using data from observational data.
  • This is because of Omitted Variable Bias.

  • When the data is not from perfectly randomized A/B test, we should utilize techniques as Control Variables : To control Omitted Variable Bias - external factors that both impact treatment assignment and dependent variable (y)

  • If we don't know how treatments are assigned (what potential bias exists in treatment assignments), we can use methods like

  • Diff-in-diff using panel data, to see if the change in trend is due to the treatment itself.
  • Instrument Variables : To control reverse causality, or external factors that influence treatment, buy not on the dependent variable (y)