Skip to content

Difference in Difference

category_specifier : "Causal Inference"

**Reference Docs: Fixed Effect

Motivation

💡How can we estimate causal effects when we don’t have an experiment? What if both treated and control groups are changing over time?

When Does Diff-in-Diff Apply?

  • When there is a policy, treatment, or event that occurs at a specific time, affecting only some units.
  • You observe two groups (treated vs. control) before and after the intervention.
  • You suspect both groups would have followed similar trends if the treatment had not occurred.

What is Diff-in-Diff?

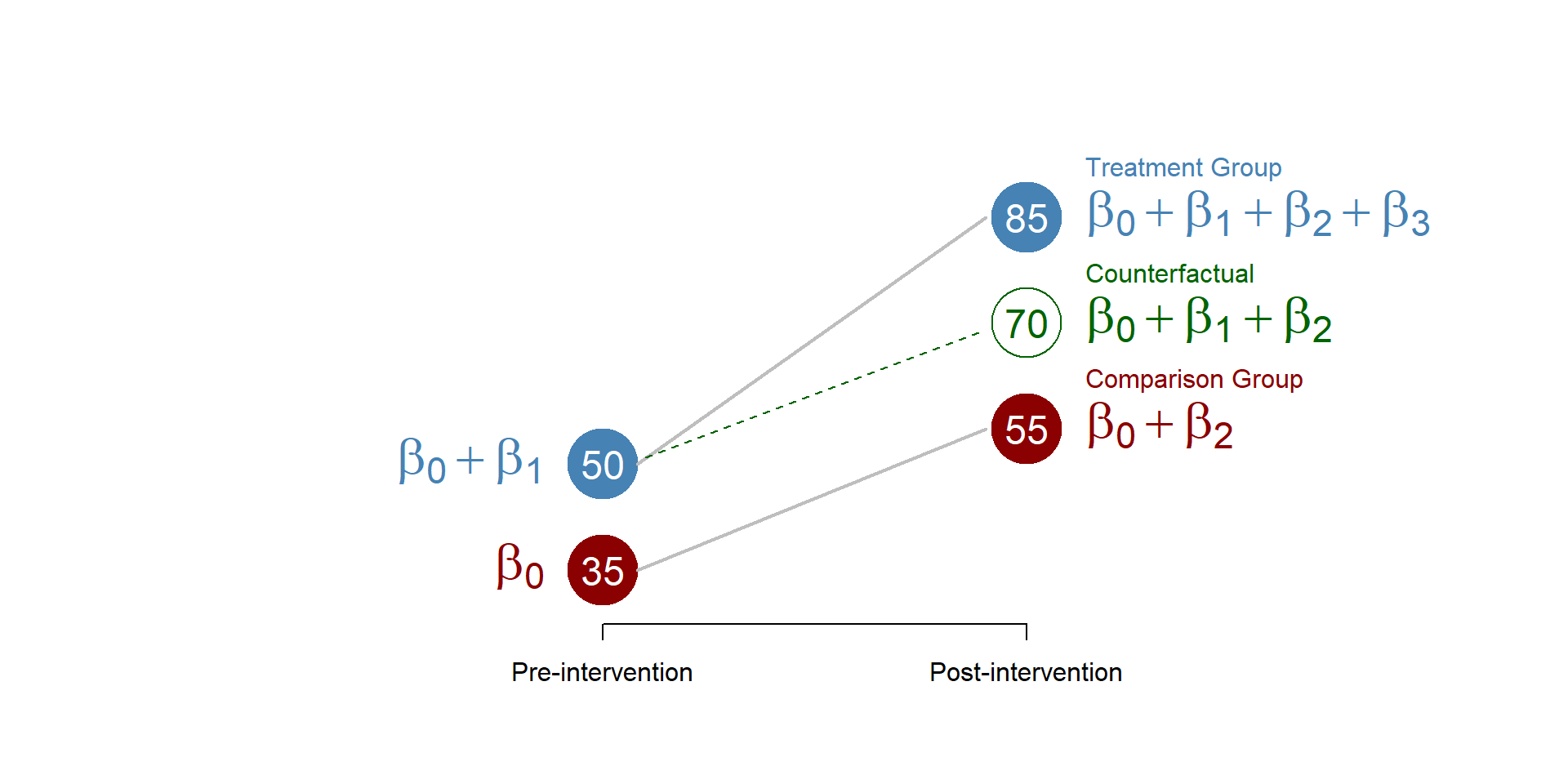
Difference-in-Differences is a quasi-experimental method that estimates causal effects by measuring how outcomes change over time between a treated group and a control group.

The method accounts for both time-invariant differences between groups and common trends that affect both groups, thereby isolating the treatment's impact.

\[ \text{DiD Estimate} = (Y_{\text{treated, after}} - Y_{\text{treated, before}}) - (Y_{\text{control, after}} - Y_{\text{control, before}}) \]

diff_n_diff

Why It Matters

Diff-in-Diff is a powerful method to make credible causal claims without randomization. It allows us to account for:

  • Baseline differences between treated and control groups
  • Time trends that affect both groups equally

This technique is widely used in policy analysis, economics, and business to evaluate the real impact of changes in the absence of experiments.

How to Apply or Extend Diff-in-Diff

Here are several ways to implement and strengthen DiD analysis:

  • Parallel Trends Check: Visualize pre-treatment trends to justify the core assumption.
  • DiD Regression Model: Estimate with interaction terms in a regression:
\[ Y_{it} = \alpha + \beta_1 \cdot \text{Treated}_i + \beta_2 \cdot \text{Post}_t + \beta_3 \cdot (\text{Treated}_i \times \text{Post}_t) + \epsilon_{it} \]
  • \(\beta_3\) is the DiD estimator
  • Two-Way Fixed Effects: Control for unit and time fixed effects in panel settings.
  • Event Study Designs: Examine dynamic treatment effects over multiple periods.
  • Placebo Tests: Apply DiD on fake treatment dates or untreated units to test robustness.

Examples

  • Soda tax introduced in one city → compare beverage sales before and after with a nearby city.
  • Company stops advertising on one platform → compare click-through rates (CTR) over time with another platform.
  • State raises minimum wage → compare employment changes with a neighboring state that didn’t.

Key Assumptions

  • Parallel Trends: In the absence of treatment, the treated and control groups would have followed similar outcome trends.
  • No Spillovers: The treatment does not affect the control group.
  • No Other Confounding Events: Nothing else happened at the same time that only affected the treated group.

Key Equations

DiD Regression Model:

\[ Y_{it} = \alpha + \beta_1 \cdot \text{Treated}_i + \beta_2 \cdot \text{Post}_t + \beta_3 (\text{Treated}_i \times \text{Post}_t) + \epsilon_{it} \]
  • \(\beta_3\) gives the causal effect of the treatment.