Skip to content

Frisch Waugh Theorem

category_specifier: "Causal Inference"

Reference Docs: Using Control Variables|Omitted Variable Bias (OVB)

Motivation

  • When there is OVB (Omitted Variable Bias (OVB)) in linear model for an experiment (or observational data for treatment effect, and want to get unbiased estimator of this treatment effect, withouth regressing with entire variabled.

Framework

FW Summary

💡When you know that the treatment is not randomizes (or partially randomized because it assigned experiment based on some characteristic, like demographic), we can use FW to control bias.

  • You did not have experiment, and do have observation data
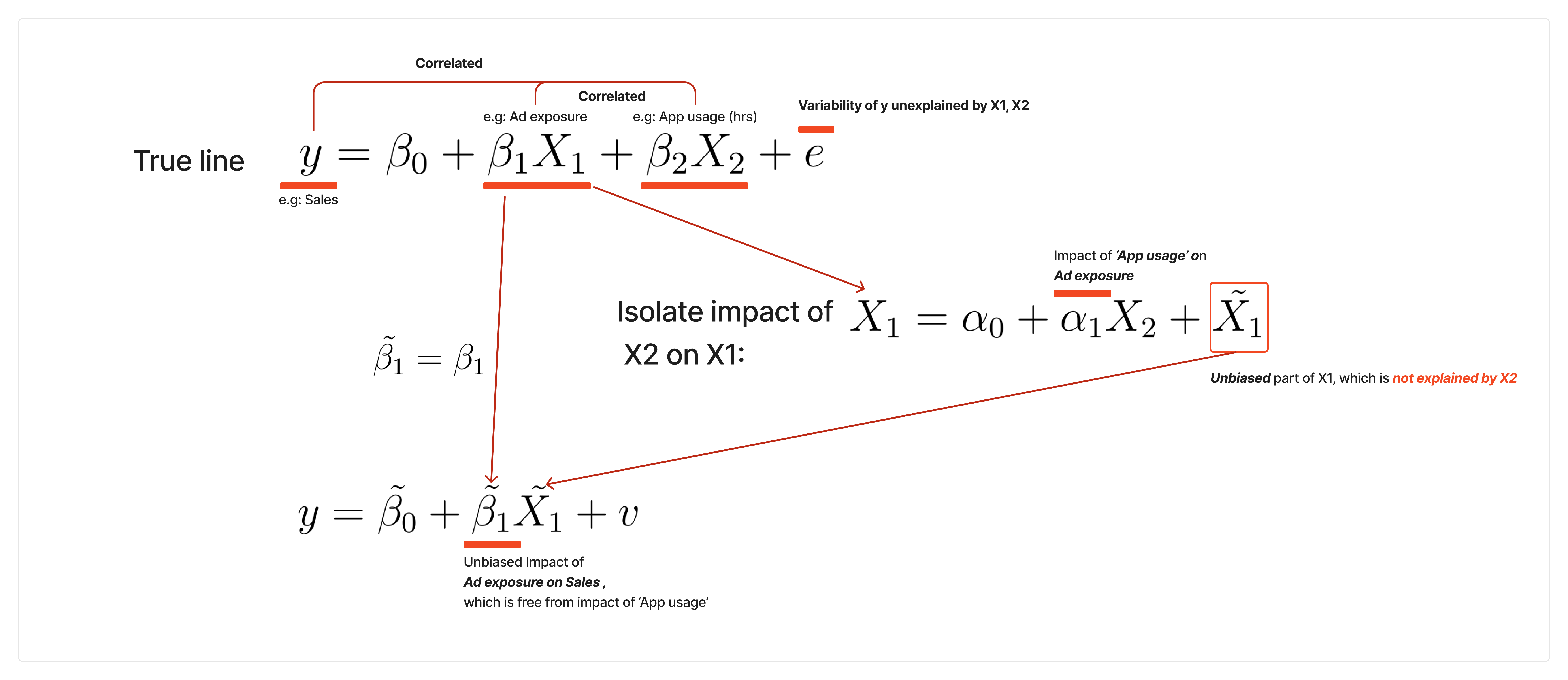
  • You assume that the following equation is true line, while \(X_1\) is treatment variable (0, 1), \(X_2\) is control variable.
\[ y =\beta_0 + \beta_1X_1 + \beta_2X_2 + e \]
  • Follow the 2-step regression below:
    1. Regress treatment on other control variables:
      • \(X_1 = \alpha_0 + \alpha_1X_2 + \tilde{X_1}\)
      • Implication of \(\tilde{X_1}\): Part \(X_1\) which is not explained by \(X_2\)
    2. Regress \(y\) on \(\tilde{X_1}\)
      • \(y = \tilde{\beta_0} + \tilde{\beta_1}\tilde{X_1} + v\)
    3. then , \(\tilde{\beta_1} = \beta_1\)